Abstract

The present digest is intended to exhibit the historical progression of the notion of ‘continuity’ from the standpoint of four different signature lines, namely Philosophers, Geometers, Arithmetizers and Topologists.

Keywords

Continuity, axiom, closeness, topology, continua, infinitesimal, continuum.

Introduction

Substratum of continuity

In calculus the first incident of tossing the word ‘continuity’ has been traced with reference to a function ?:R?R . In calculus, we have seen that the limit of a function ?(x) , as x?a  can often be found by computing the value of the function at the point a . Functions possessing such a property are called continuous at a . The most popular device for continuity, that is prominently being adopted by entire modern mathematical community is mentioned as below.
       
           
            

Figure 1: Screen of motivation for continuity

Calculus device for continuity- A function ?(x)  is continuous at a number a  if the following three steps hold.

2437468. ?a  is defined (i.e., a  lies in the domain of ? )

215737630. limx?a?x  exists (i.e., ?  must be defined on an  

                open interval containing a ).

8811430. limx?a?x=?(a)

However, like the convergence, function’s continuity has been a subtle and extremely important notion which is not only utilized in Calculus, but in almost every branch of mathematics. In fact, continuity is probably the single most important concept in all the mathematical premises. Admitting in mind that ‘a function is a way to walk from one set to another’, or speaking topologically, ‘a function is a way to transform one topological space into another’. When the function is continuous, most of the crucial features that the domain space possesses (e.g., like being all in one piece, being open, being closed, being compact etc.) are maintained into their existential form, under the transformation, so that the image space could also retains these features. This kind of preservation of such crucial features is of the utmost importance in topology. Such an act of preservation of crucial features of mathematical objects by the continuity of mathematical function is being practiced by human being in many senses. For instance, now a days we are giving emphasis upon ‘sustainable use of natural resources’-which straightforwardly means- using natural resources without harming the nature, i.e., being aware of “human act (function) to mother nature (domain) so that the quality (being natural) of codomain (mother earth) remain intact” 

The pragmatic and splendid outcome of continuity in almost all the mathematical disciplines is that “any shape, maintaining its continuity can be elucidated by a single equation”. However, if there are fractures or interruptions in continuities of shapes (e.g., sharp edges and singularities etc.), then more than one equation would be needed to define the fractured parts of the shape under consideration. In spite of continuity being a highly insisted device specifically offered by calculus and Topology, from aesthetic point of view, it is sometimes felt necessary to break the seamless-ness of shapes, so that more advanced and beautiful shapes could be evolved (e.g., evolving particular geometric structures by breaking the continuity of flat surface material).

The present digest is focused on exploring the concept- ‘continuity’, from the various dimensions of history. More explicitly, it has been tried to nest the historically generated thoughts, ideas, axioms, definitions and results regarding continuity. In particular, the standpoints of Philosophers, Geometers, Arithmetizers and Topologists have been referred to weave the fabric of the ‘continuity’.

2. ‘Continuity’ in the time of Aristotle and Euclid

Henri Poincaré in 1905 held that- ‘primarily, what properties of ‘space’ are responsible to call the so-called space a ‘mathematical space’? In response to this question, he evoked three of the properties of any mathematical space, namely:

1. It is continuous
2. It is infinite
3. It is of three dimensions

Perhaps, the emergence of clearer ideas of ‘continuity’ gradually came into full swing from 17^th century onwards, wherein the literal meaning of the world ‘continuity’ had been assumed to be “seamless, unbroken, uninterrupted or ceaseless”. And thus, the mathematical entity, which in modern mathematics is called the ‘continuum’ is assumed as an ‘unseparated or pause-less or cavity free thing’. Further, it has been heuristically supposed that most of the physically phenomena such as displacement, velocity, growth of living entity etc. are continuous in nature as they vary with time. Even, many philosophers have evoked that space and time and natural processes occur continuously, for instance, Leibnitz made a famous argument that “nature makes no jump”. The geometrical entities such as lines, planes and solids have also been considered either as aggregations of infinitesimal parts or the accumulation generated by the flow of some entity. However, there are the situations where this argument gets infringed- e.g., the discontinuity occurs in case of electric current.

Besides the above contemplation on ‘continuity’, if we switch back history, we can find a long lasting and vibrant debate over this issue. The very first emergence of ideas of ‘continuity’ and ‘infinitesimal’ in mathematics can be found with Greek atomist philosopher Democritus (450 BC) and then with Eudoxus (350 BC). The doctrines, they followed in delineating ‘continua as infinitely divisible entity’, is now familiar to us as ‘divisionism’. At the prima facie, the approach of ‘divisionism’ encapsulates a long chain of logics and is being discussed in the following subsection (2.1).

1. 1. Prima facie of ‘divisionism’

Observations made by Democritus and Eudoxus have been interpreted by (J. L. Bell, 2005a) as follows:

• The very nature of the ‘continuum’ or the ‘continua’ is- being indivisible or unbreakable.  But the seamlessness or the unity of continua never implies that its ingredients are not divisible. In fact, the indivisibility of continua means that endless recursive division of it is always possible. That is the entity which can be divided everlastingly. Thus, the basic characteristic of continua is that- such an entity can be decomposed into ever smaller entities, provided the process of decomposition never terminates.  One can explicitly think of continuum as;

‘continuum’ ?  an entity consisting of entities which are ‘continuum’ themselves

• The witness, for example in nature, could be the magnet- as if we crush it and even turn it into powder form, even then each of its corpuscle shall retain the property of magnetism. Further, to feel the potential of continuum, one can consult the fractal analysis (see figure-2)

       
           
       
    Figure 2 motivational pictures of 'continua' where each part of these pictures can be endlessly divided into ever smaller parts.

• The infinitesimal magnitude of the continuum can be informally conceived as a continuum itself, i.e., the smallest possible parts of the continuum can be though superficially as a continuum. 
• The philosophy of continuity gives rise the sense of ‘being connected’

2.2 Aristotelian standpoint to continuity

Drawing inspiration from the logical chain of the thought held by Democritus and Eudoxus, Aristotle (384-322 BC) proposed an idea that- ‘the theme infinitesimal is tangled with the notion of continuity’. Soon, this idea led him to the flowing arguments:

• With his geometrical signature line, Aristotle made an observation that- “Nothing that is continuous, Aristotle held, can be composed of indivisibles”. (Evans, 1955)
• Behind this, Aristotle gave the logics that- as time is not constituted of instances, likewise a line is not constituted of points, because both the time and line are continua. Also, by continua, he meant that- “which is divisible into divisibles, that are further divisible”
• He proposed that a continuous magnitude is- ‘that allows it to be dissected into infinite number of parts.
• It was made clear by him that though a line cannot be dismantled into infinite number of pieces, even then it is an aggregation of infinite number of points, and thus it retains continuity.
• From the above supposition, it becomes precise that, as per geometrical viewpoint of Aristotle- the continuity of a line entirely depends upon the continuity of motion.
• He further argued that-continuous magnitude is perceived due to ‘motion’ and therefore, ‘it is the motion, which is directly responsible for the generation of continuous magnitude’. For, clear understanding, he mentioned an example- A moving point generates a line and a moving line generates a surface.
• With the above ideas, Simplicius(Urmson, 2014) (Baltussen et al., 2014)  rephrased Aristotle’s principle in a nutshell as:

“A line is the fluxion of the point”

Eventually, Aristotle in his book ‘Aristotle’s Physics’ ended his quest for continuity with two criteria, as follows:

• Aristotle’s criteria for continuity: Aristotle said that- something is said to be continuous if

• The entities or things whose limit, at which they touch, is one(Lang, 1992) 
• That thing or entity, which is divisible into what is always further divisible(Sachs, 1995)

3. The Axioms of continuity- in the time of Euclid

The great flux of logics over continuity, continua and infinitesimal, propagated from Democritus (450 BC), Eudoxus (350 BC), Aristotle (384-322 BC) and Simplicius (490-560 AD) led Euclid (300 BC) to refine his fundamental propositions of geometry, which he quoted in his famous book Euclid’s Element(Euclid, 1956). Indeed, Euclid found axioms of continuity as a suitable tool to minimize the number of pauses in his postulates of geometry. One of his first postulates, which he refined with the aid of ‘principle of circular continuity’ can be taken into consideration as an example here. Consider the following arguments, which Euclid gave to justify his first and foremost proposition:

3.1 First and the foremost proposition of Euclid

Postulate (I): “Given any segment, there is an equilateral triangle having the given segment as one of its sides”(Conover, 2014) (Greenberg, 1993) (Thomas & Thomas, 2003) (Heath, 1926)

 Proof: Starting the proof with the fundamental idea on the construction of ‘line’ would help us understating the more complex proof to the present postulate. (Longo, 2012),  (Longo, 2015) has fantastically analyse and synthesize upon the construction of the first fundamental structure of Greek Geometry. 

If we simply go through the Euclid’s book of Geometry, we can easily observe that in the entire Greek Geometry, the invention of first and fundamental mathematical structure has been the ‘line with no thickness.’ In fact, no Euclidean line is possible without acting a trace and without no thickness (Longo, 2015). Clearly a gesture alone or logic alone cannot describe the line. This simply means that ‘lines are ideal objects’ and thus they can be thought to be a cohesive continuum with no thickness (Longo, 2012).   In Euclidean geometry- when two thick-less (1-dimensional) lines suitably intersect with each other, produce a point (no-dimensional structure). With these much of fundamental structures, Greek geometry moved towards the invention of continuous lines with no thickness and the geometer called such a construct-an abstract divine construct. (Longo, 2012) synthesized that- no matter, a line is continuous or discrete, it is always a gestalt rather than a set of points.   

For the sake of convenience, let us now sketch the proof of Euclid in a step-by-step sequence of logics as follows:

Step 1- Let PQ be any given line segment. Now, with centre P and radius PQ, describe a circle QRS (under Euclid’s 3rd postulate, see(Euclid, 1956) (Heath, 1926)) (See Figure 3)

Step 2- Again, by assuming Q as a centre and QP as radius, we can describe another circle PRT using the same Euclid’s postulate-III(Euclid, 1956) (Heath, 1926)].  (See Figure 3)

       
           
            

Figure 3: Notion of Circular Continuity under Euclid’s postulate-III

Step 3- From a point R, at which the circles C1 and C2 intersects each other, sketch the line segments RP and RQ (under the Euclid’s postulate-I(Euclid, 1956) (Heath, 1926) ).

Step 4- Now, because P is the centre of circle C1 and Q is the centre of C2, PR will be congruent to PQ (in view of circle’s définition).

Step 5- Similarly, Q being the centre of circle C2, clearly QR will be congruent to QP due to the definition of circle.

Step 6- Finally, since RP and RQ are congruent to PQ (due to steps 4 and 5),

Step 7- Consequently, the ?  PRQ is an equilateral triangle, having PQ as one of its sides.

Observation- Now if we keenly look back each of the logical steps we outlined above, it seems that the proof is flawless. But observing the 3^rd step above, we conclude that our belief on the fact ‘that two circles intersect each other at point R’ is due to the diagram drawn (Figure 3). It means if we do not allow ourselves to use diagram, the step 3^rd become less explicit and therefore, we need some additional axiom to prove that circles described in the proof of Euclid’s first proposition intersect each other.

Thus, to make step 3^rd more precise or explicit, let us go through the principle of circular continuity.

Definition-1: Principle of circular continuity

This statement enunciates that “If a circle C1 has one point inside and one point outside another circle C2, then the two circles intersect at two points.”

In circular continuity, the notion of ‘inside/ outside’ a circle is utilized by stating that a point U is inside a circle having centre O and radius OV  if OU   and the same point lies outside if OU>OV .

The notion of ‘inside/ outside’ can be made precise with the assistance of elementary doctrine of continuity, which states the following:

Definition-2: Elementary doctrine of continuity

“Consider a segment of straight line. If one end point of this segment lies inside a circle and other end point outside the circle, then such a segment intersects the circle.”

But what makes the above two principles-the continuity principles? The answer must be in the geometry sketch (See Figure A2), wherein a line segment with the help of a pencil is drawn by moving the pencil continuously from a point P to Q. It’s very much obvious that such a drawing should traverse a circle having centre say O and it’s also natural to say that if, it does not happen like this, there must be a ‘hole’ present either on the line segment or on the boundary of circle.

       
           
            

Figure A2: (a): geometrical interpretation of elementary continuity, where a line segment PQ is drawn by moving a pencil and the segment traverses through the circle. (b): geometrical interpretation of discontinuity due to a hole being present on the line segment PQ. (c): geometrical representation of discontinuity due to a hole being present on the boundary of circle.

One strange thing from Euclid’s ‘Eléments’ that mesmerize the mathematicians is- the use of actual construction geometry as a device for figures and diagrams bearing certain characteristics. Thus, geometric constructions were affected by drawing of straight-line segments and circles as per the guidelines of postulates 1 to 3 of Euclid’s and the extract of this kind of construction was to determine new line segments, circles and so on from the points of intersections of lines and circles. But, the intersection of such line segments and line segments with circles, so as to determine new lines and circles gave rise a question of existence of intersection points and thus the quest for a new kind of existential postulate was started.   

Killing  tried to assist the existence of intersection points by putting forward two rules(Killing, 1892):

3.2 Killing’s rules for the existence of intersection point:
Rule-I: Suppose a line belongs completely to a geometric figure which is dissected into two parts; then, if the line has at least one point in common with each part, it must also meet the boundary between the parts.

Rule-II: If a point moves in a figure which is divided into two parts, and if in the beginning of motion, it belongs to one part, and at the end of the motion, it pertains to the other part of figure, then meanwhile the motion of point, the point must reach at the boundary between the two parts.

4. Continuum, infinitesimal and continuity in 17^th & 18^th centuries

Trailing the ideology of Democritus (450 BC), Eudoxus (350 BC), Aristotle (384-322 BC), Simplicius (490-560 AD) and then Euclid (300 BC), 17^th and 18^th century philosophers and mathematicians such as, Kepler, Galileo, Newton, Marquis De Hôpital, Leibnitz, Euler, Barrow and Kant tried to establish a systematical construct of relations among continuity, continuum and infinitesimal.

Moreover, especially in 17^th century, mathematicians coined the following prominent thoughts:

17^th century mathematicians held that-

• Continuous curves are made up of infinitesimal straight lines’ and therefore the continua’s (which is thought as a unity) constituent parts must be continua themselves.’
• Since entities like points are non-decomposable or indivisible, thus, they cannot be the parts of any continuum.
•  Any number may be supposed as an infinitesimal number, if it does not coincide with the number zero and if in some sense, it remains smaller than any finite number.
•  In Newtonian calculus, infinitesimal quantities were treated as ‘instrumental’.
• From Leibnitz’s perspective, the infinitesimal quantities were supposed to be ‘unassignable quantities.
• As per the treatise of Marquis De Hôpital, entitled ‘Differential Calculus’ published in 1696, it was postulated that- “a curved line may be regarded as a composition of infinitely tiny straight lines” and “one can take any two quantities equal, provided they are differ by an infinitely small quantity”
• Isaac Barrow (C.1630-1677), an English mathematician, while developing method for finding tangents realized that- notion of infinitesimal is an essential tool for his method and thus he introduced two mesmerizing words “Linelets” and “Timelets” for infinitesimal, which appeared later in his work “Lectiones Geometricae” in 1670.   

However, among the 17^th century philosophers and mathematicians, the British mathematician sir Isaac Barrow (1630-1677) has been credited as a pioneer in defining the continuous magnitude in a systematic way. Barrow begun to establish a reciprocal relation between the problem of quadrature and that of finding tangents to the curves and he drew the following conclusion:

1. 1. Barrow’s conclusion(s)

Barrow, in his work “Lectiones Geometricae” in 1670 observed that(J. Bell, 2004)-

1. If for any curve y=?x , the quadrature be known with the area given by ?x , then the subtangent of the curve y=?x  can be determined by measuring the ratio of its ordinate to the ordinate of original curve y=?x , i.e., subtangent of ?x=ordinate of ?xordinate of ?x .
2. Because, continuous magnitudes are generated due to motion, therefore they essentially be dependent on time.

Sir Isaac Newton (1642-1727) during the plague pandemic, deeply deployed the tools (a) and (b) of his teacher Barrow, and consequently established his work, now popularized as “Calculus of fluxions”. He, thus pave the way to a new paradigm of continuity(J. L. Bell, 2005b).

1. 2. Isaac Newton’s calculus of fluxions

Here are the notions, that Newton apprehended in his work-

-47.  As Newton supposed the infinitesimal quantities to be just instrumental in his calculus, he notified these instrumentals as “Momentary increments”. Probably, such notification was because of utilizing kinetic notions in his work.
-46. For him the “momentary increment” means an instance of time, or a moment of time- of abscissa or the area of the curve with the abscissa (abscissa itself stands for time in this case)
-45. Newton introduced the symbols-

o?abscissa , v?ordinate , ov?area of the curve .

Probably these symbols infer that, Newton’s supposed a curve to be a plot or graph between velocity and time.  

-44. Taking into account a moving line or an ordinate, as a moment of   area of the curve, Newton established a generalized result for the reciprocal relation between the differentiation and the integration.
-43. Finally, in his work “Methodus fluxionum”, Newton had introduced the variable quantities generated due to motion as a “fluent”. He evoked the rate at which quantities “fluent” were generated, as a “fluxion”.
-42. The notations, he notified in his calculus were denoted by-

fluxion of the fluent? x ,moment of fluxion?xo

In the meanwhile, Gottfried Wilhelm Leibnitz (1646-1716), a German polymath was intensively working on ‘a general law of continuity’ and he was literally provoked by the question that- what composes the continuum? He cited this problem as “Labyrinth of the continuum”.

1. 3. Leibnitz’s monadism and law of continuity(J. L. Bell, 2005a)

G.W. Leibnitz, in his quest for the principle of continuity, walked through the problem that- whether a continuum can be built from indivisible entities? If yes! Then how? In search of answer, he put forwarded a new philosophy called “Monadism”, which led him to the following conclusions-

-47. Leibnitz inquired himself that-if every real entity is supposed to be either as a ‘unity’ or as a ‘multiplicity’, and further, if ‘multiplicity’ be essentially treated as an accumulation of ‘unities.’ Then under what characteristics and in what category, a geometric continuum (e.g., a line, surface or a solid) should be placed? 
-46. He further argued for example, that-if a line is extended, and an extension being categorized as recursion, then a line cannot be treated as a true ‘unity’, as it is divisible into parts. Hence, rather a true ‘unity’, a line is true ‘multiplicity’.
-45. Leibnitz concluded the 2^nd argument under the influence of the already established logics that state- (a). The only unities of any geometric continuum could be points, but points have no further divisibility attitude and therefore, points are not more than the extremities of the extension of line

(b). Also, according to Aristotle- “no continua can be composed of points”   

-44. With the aid of argument 2^nd and 3^rd, Leibnitz came to assert that- “Continua is neither a unity nor a multiplicity”, which literally means that, in practice, there does not exist anything like real continuum, which is either unity or an accumulation of unities.
-43. Eventually, he founded that-space and time, in ideal situation can though to be as continuum. However, anything which is real (for example matter) always reveals the discreteness as being composed of substance like units and he notifies such simple units as “Monads”   

But what makes Leibnitz enforced to think upon infinite numbers? In fact, the answer is hidden in the work of Galileo Galilei, who in his ‘Two new sciences’ proposed that (Arthur, 2015)-

1. “The matter is composed of an actually infinite number of atoms.”
2. “And each of the atoms are separated by infinitely small voids.”

Leibnitz followed the idea of Galileo Galilei that ‘in the infinite, there is neither greater, nor smaller’ and demonstrated this as follows(Leibniz, 2001):

“Among numbers, there are infinite roots, infinite squares, infinite cubes. Furthermore, there are as many roots as numbers. And there are as many squares as roots. Therefore, there are as many squares as numbers.”

Leibnitz, from the above quoted demonstration concluded that- there are as many square numbers as there are numbers in the universe, which is impossible. Consequently, in the infinite, the whole is greater than the part, which is the affirmation of Galileo. 

To validate Galileo assertion that ‘the whole is greater than the part’, Leibnitz finally produced a purely mathematical version (Arthur, 2015). What he did in this mathematical version is:

1. He drew a symmetrical diagram (see Figure 4a), which he called Leibnitz’s hyperbola with centre A and vertex B. Then he sat AC = BC = a or 1 without loss of generality.
2. Then he tried to determine the area under this symmetrical curve between the line CB & X-axis
3. To do so, he used DE = 1/ AD = 1/ (1-y), which he expanded in terms of power series as: DE=1AD=11-y=1+y+y2+y3+?
4. Then he calculated the area in question by applying the variable line DE to the line AC = 1, which yield: Area (ACBEM)= 1+12+13+14+? . As per the modern mathematics, Leibnitz has integrated the power series as 011+y+y2+?dy
5. In a similar fashion, he calculated AreaCFGLB=1-12+13-14+?
6. Finally, he subtracted the finite Area (CFGLB) from the infinite Area (ACBEM) to get- Area ACBEM-Area CFGLB=Area ACBEM
7. It was more than enough to demonstrate that subtracting an area (i.e., Area CFGBL), which is definite and explicitly perceivable, from the area under the hyperbola (i.e., Area ACBEM) leaves the Area ACBEM intact. Which shows that the whole is greater than the part.

       
           
            

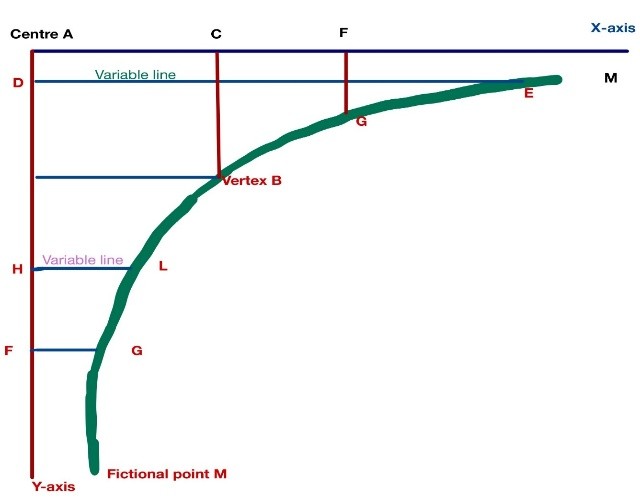
Figure 4a: Leibnitz’s Hyperbola

With this philosophy of “monads”, Leibnitz presented one of his best doctrines, now known as ‘principle of continuity’.

1. 4. Leibnitz’s principle of continuity(Heath, 1926)

The mathematician contemporary to Leibnitz established some important facts pertinent to the tangent to some given curves, and they granted that ‘one could find a tangent line at every point of a curve under consideration’. Basically, they developed a geometric construction wherein they assumed that- given a curve and a point P  on the curve, the tangent line can be constructed by passing a line through P  and another point Q  lying on the curve. Further, any point Q  which is differ from P  will also yield a line, because in accordance with the Euclid’s postulate-I, ‘Any two points determine a line’. To obtain a tangent line, mathematician followed idea of nearness/ closeness as prescribed by Leibniz and they moved point Q  close enough/ near enough to P .
Such a beautiful construction was later formulated as a general principle and now known as Leibniz’s continuity principle:

Definition-3: Continuity principle- “In any supposed transition, ending in a terminus, it is permissible to institute a general reasoning, in which the final terminus may also be included”.

However, this principle got stuck when few counterexamples came into existence in the course of study. One of them was as follows:

 Example 1: Let us consider the function fx=x , where the symbol .  stands for absolute value which is usually defined as: x=x  if x?0  and x=-x  if x<0> . It’s obvious from the graphical representation of this function that the function lies in the 1^st and 2^nd quadrant of the plane. Clearly, for each non-negative value of x, the absolute value function has a tangent that coincides with fx=x . However, for each negative value of x , the absolute value function has a tangent that coincides with fx=-x .

Now in view of Leibnitz’s continuity principle, in the process of drawing tangent, it might be possible to extend towards the origin and hence the origin should be the terminus. However, if we proceed drawing tangent from the right of the origin, the tangent at origin must coincide to the line y=x , i.e., the gradient must be +1. Likewise, if we proceed to draw tangent from the left of the origin, the tangent at origin must coincide with the line y=-x , i.e., the gradient must be -1. Therefore, the tangent at origin is impossible to define, because a tangent at some given point cannot have two different gradients at the same time.  

Apart from the above graphical approach, the same conclusion that ‘Leibnitz‘s continuity principle’ ceased for the function fx=x , can be drawn using the simple device of Calculus as follows:

Example-2: Consider the function fx=x  and let us try to show that Leibnitz’s continuity principle fails to hold, specially at (0, 0). For this, let us determine the derivative of given function via implicit differentiation. Suppose ddxfx=ddxx.  Making use of chain rule; ddxfx=dfudududx.  Where u=x , and ddufu=f'u . Then ddxxf'x=ddxx . Since the derivative of x  is 1, therefore f'x=ddxx . Again, in implementing chain rule:
ddxx=dudu.dudx , where u=x  & dudx=uu . Thus, f'x=xd/dxxx , and again derivative of x  , with respect to x  becomes 1, so we finally have: f'x=xx , which yields +1, when x?0  and -1 when x<0>

       
           
            

Figure (4b): The gradient to the curve in the first quadrant of the plane is +1, whereas that of the curve in second quadrant is -1. This holds true to each point of either of the curves. In view of Leibnitz’s principle of continuity, it is observed that derivative at origin does not exist.

A plenty of such curves having corners or cusps, were soon encountered by mathematicians and they believed that points where derivative did not exist were exceptional. Mathematicians also found hard to imagine the curves which entirely consist of cusps or sharp corners. To imagine and draw jagged curves, prior to calculus it would be heavily required to introduce Topological notions.  

Let us switch back to the time, when Leibnitz exploited his continuity principle in developing his infinitesimal calculus. Leibnitz wrote essay “Nova Methodus” in 1684 which was followed by another essay “De Geometri Recondita” in 1686, wherein he formally introduced the notion of differential and integral calculi. In these two essays, he included the following:

1. He supposed a curve characterized by two correlated variables, namely x & y
2. Then, he notified symbols dx & dy  to formulate the infinitesimal differences or the differentials between variables  x & y .
3. Further, he notified a symbol dxdy  for the ratio of the above two differences and he called this as ‘slope of the curve at a point.’
4. Though, infinitesimal differences for Leibnitz were unassignable quantities, he in 1684 proposed the following rules without demonstration:

• d?=0
• d?x=?dx
• dx+y-z=dx+dy-dz
• dxy=xdy+ydx
• dxy=ydx-xdyy2
• dxn=pxp-1dx

5. When, Leibnitz felt the essential admittance of incomparably tiny quantities, which were seemingly small than the ordinary numbers-he argued that, law of continuity governs the incomparably small quantities in the similar fashion as it governs the ordinary numbers.
6. Ultimately the argument (V), forced him to involve the infinitesimal quantities with finite quantities. But he always treated the infinitesimal quantities as if they were zero. Thus, for instance, Leibnitz treated the quantity x+dx  same as x . Such a treatment, he followed was based on the notion that ‘differentials cannot be stagnant, rather they should be variables and should be diminishing continuously until arrived at zero’.
7. He developed his calculus with the notions that-

• Differentials or infinitesimal are neither something nor equal to the absolute zero.
• dx?0 , by which he meant that differentials are indistinguishable from absolute zero
• Neither dx=0 , nor dx?0
• dx2=0
• dx?0 , by which he meant that the differential is vanishingly small.

4.5 Euler’s refutation to Leibnitz’s monadism

A Swiss polymath Leonhard Euler (1707-1783), while practicing calculus straight away refuted the Leibnitz’s monadism by involving the Cartesian principle in his study.

As its well known that- the theory of monads or simple things of which the body is composed, relies upon two general features of the bodies, namely; ‘extent & the moving forces’ (Haude & Spener, 1746). Euler argued that, such a theory can be true if the arguments leading to it are valid. With this quest, Euler has set up deepen exploration towards the Leibnitz’s theory to arrive at the following concluding remarks:

1. Regarding the first property of monads, i.e., ‘extent’, Euler said that- it is undoubtedly true that all bodies are composed of parts and that these ever-smaller parts can be distinguished. Because, if through decomposition, we eventually reach at a particle so small that with naked eyes the particle is observed to have no further parts; then it can further be examined with a magnifying glass to discover that the particle still has a large number of real parts.
2. Euler questioned that- whether this long-lasting divisibility can be continued infinitely far? Or whether this decomposition process reaches at some limit, such that there remain particles with no size? Indeed, these questions are still a matter of debate. 
3. Regarding the second property of monads, i.e., ‘moving forces’, Euler proclaimed that- since every-body have such a force to remain in its natural state, the cause of this force must be found in the essence of the body. Thus, it can be rightly concluded that every-body is endowed with a force to remain in its present state.
4. Euler submitted that- the force which is responsible to retain the body in its current state is called ‘Vis inertiae’.
5. He further claimed that in the theory of movement, the force ‘Vis inertiae’ is generally a property of the body without which a body ceased to be a body. 
6. Thus, Euler gave the reason ‘inertia’ for the change in the world, while dealing with the query that ‘Why there are continuous changes in the world?’
7. Euler further refuted the Leibnitz’s notion of infinite divisibility by mentioning that- ‘Mr. Leibnitz appears to admit infinite divisibility by maintaining that infinitely many monads shall be required to represent the smallest body’. However, this statement contradicts itself, as this one is equivalent to saying that- ‘bodies can through no division, however far this might be continued, be subdivided into such simple things, through which in fact the existence of simple things is denied.’
8. Euler also argued that- if we assume that a body is composed of simple things, then we should acknowledge that the number of these simple things is definite. But if one takes this number to be infinite, it can be no more definite and therefore infinitely huge would mean a magnitude beyond understanding.
1. Thus, Euler summed up the crucial difference between his own and Leibnitz’s definitions of infinitely small quantities in the following way (Knobloch,2008):
   (a).  Suppose i  be an infinitely small quantity, gq  be a given quantity and aq  be an assignable quantity, then:  

(b). Leibnitz- for all gq>0 , there is an igq>0 , so that igq<gq igq  is a variable quantity.

(c). Euler- for all i  and for all aq>0:i<aq, i=0      

References: 

1. Arthur, R. T. (2015). Leibniz’s actual infinite in relation to his analysis of matter. GW Leibniz, Interrelations between Mathematics and Philosophy, 137–156.
2. Baltussen, H., Atkinson, M., Share, M., & Mueller, I. (2014). Simplicius: On Aristotle Physics 1.5-9. A&C Black.
3. Bell, J. (2004). Hermann Weyl’s later philosophical views: His divergence from Husserl. Husserl and the Sciences, 173–185.
4. Bell, J. L. (2005a). Continuity and infinitesimals.
5. Bell, J. L. (2005b). The continuous and the infinitesimal in mathematics and philosophy. Polimetrica sas.
6. Benjamin, B. C. (1968). A History of Mathematics. New York, NY, United States of America: John Wiley & Sons Inc.
7. Berkeley, G. (n.d.). The Analyst, a Discourse Addressed to an Infidel Mathematician. Strand, London, England, 1734.
8. Berkeley, G. (1754). The analyst; or, a discourse addressed to an infidel mathematician: Wherein it is examined whether the object, principles, and inferences of the modern analysis are more distinctly conceived, or more evidently deduced, than religious mysteries and points of faith. J. and R. Tonson and S. Draper.
9. Bishop, E. (1967). Foundations of constructive analysis.
10. Bolzano, B. (2012). Paradoxien des unendlichen (Vol. 630). Felix Meiner Verlag.
11. Boyer, C. B. (1940). The concepts of the calculus: A critical and historical discussion of the derivative and the integral. Mind, 49(194).
12. Connell, A. F. (2022). Unforeseen Asymmetries: A Contemporary Mathematical Reading of Kant’s Second Antinomy.
13. Conover, R. A. (2014). A First Course in Topology: An Introduction to Mathematical Thinking. Courier Corporation.
14. Euclid. (1956). The Thirteen Books of Euclid’s Elements. Courier Corporation.
15. Evans, M. G. (1955). Aristotle, Newton, and the Theory of Continuous Magnitude. Journal of the History of Ideas, 548–557.
16. Greenberg, M. J. (1993). Euclidean and non-Euclidean geometries: Development and history. Macmillan.
17. Haude, A., & Spener, J. C. (1746). Gedancken von den Elementen der Cörper, in welchen das Lehr-Gebäude von den einfachen Dingen und Monaden geprüfet, und das wahre Wesen der Cörper entdecket wird. bey A. Haude und Joh. C. Spener, Königl. und der Academie der Wissenschaften ….
18. Heath, T. L. (1926). The Thirteen Books of Euclid’s Elements. Translated from the Text Heiberg (Vol. 1). Cambridge University Press.
19. Hocking, J. G. (1961). G. s. Young. Topology, 31–48.
20. Jankowiak, T. (2020). Kant on the Continuity of Alterations. Canadian Journal of Philosophy, 50(1), 49–66.
21. Killing, W. (1892). Ueber die Grundlagen der Geometrie.
22. Knobloch, E. (2008). Generality and infinitely small quantities in Leibniz’s mathematics-The case of his Arithmetical quadrature of conic sections and related curves.
23. Krantz, S. G. (2009). Essentials of topology with applications. CRC press.
24. Lang, H. S. (1992). Aristotle’s Physics and its medieval varieties. Suny Press.
25. Laugwitz, D. (1987). Infinitely small quantities in Cauchy’s textbooks. Historia Mathematica, 14(3), 258–274.
26. Leibniz, G. W. (2001). The Labyrinth of the Continuum: Writings on the Continuum Problem, 1672-1686.
27. Longo, G. (2012). Theorems as constructive visions. Proof and Proving in Mathematics Education: The 19th ICMI Study, 51–66.
28. Longo, G. (2015). Synthetic Philosophy of Mathematics and Natural Sciences Conceptual analyses from a Grothendieckian Perspective. Speculations: Journal of Speculative Realism.
29. Mendelson, B. (1990). Introduction to topology. Courier Corporation.
30. Munkres, J. R. (2000). James R. Munkres Topology Prentice Hall, Incorporated, 2000.
31. Sachs, J. (1995). Aristotle’s physics: A guided study. Rutgers University Press.
32. Thomas, K. W., & Thomas, A. T. (2003). Commentary on Aristotle’s Physics (Vol. 1). A&C Black.
33. Urmson, J. O. (2014). Simplicius: On Aristotle Physics 5. A&C Black.
34. van Strien, M. (2015). Continuity in nature and in mathematics: Boltzmann and Poincaré. Synthese, 192, 3275–3295.
35. Watkins, E. (2006). On the necessity and nature of simples: Leibniz, Wolff, Baumgarten, and Kant. Philosophical Studies, 132(2), 215-240.